Sign up

To sign up as a hunter, email at tokarsky@ualberta.ca and we will send you a region to cover. There is no point in having the same person covering the same region. Once it is done and proved, we will post your name on the list. If you dawdle, we will assign it to someone else who is interested.

A project by George Tokarsky, Austin Lu, Bhavya Jain and Kaiden Mastel.

2024 News Flash!

New Jars for Billiards Everything and Billiards Covers which go much faster! These can be downloaded below or at sourceforge.net
New Game found at "thegreatperiodicpathhuntgame.vercel.app" Discover new covers and be recognized and earn points.
New Periodic path cover with vertices (6,29), (10,25), (10,35), (6,39) These latest covers are now on Billiard Covers.
New Buttons on Billiards Everything which go 2-4 times faster or more by making use of your threads.
New Buttons automatically insert the codes into the cover.
New Instructions which include all these new buttons SuperAustinVary, AustinMaxVary, BoyanVary, VaryL.

2023 News Flash!

New The Hunt now allows the use of Windows or Linux as well as Mac.
New Periodic path cover with vertices (6,39), (10,35), (10,57.6), (6,61.6).
New AutoPolyVary button automatically fills holes.
New Triples button makes it easier to find triples.
New Can now load multiple covers.
New Instructions and two new videos.
New Jars for Billiards Everything and Billiards Covers.
New A new cover for Schwartz's 100 degree theorem (using 186 regions! instead of 215).

2022 News Flash!

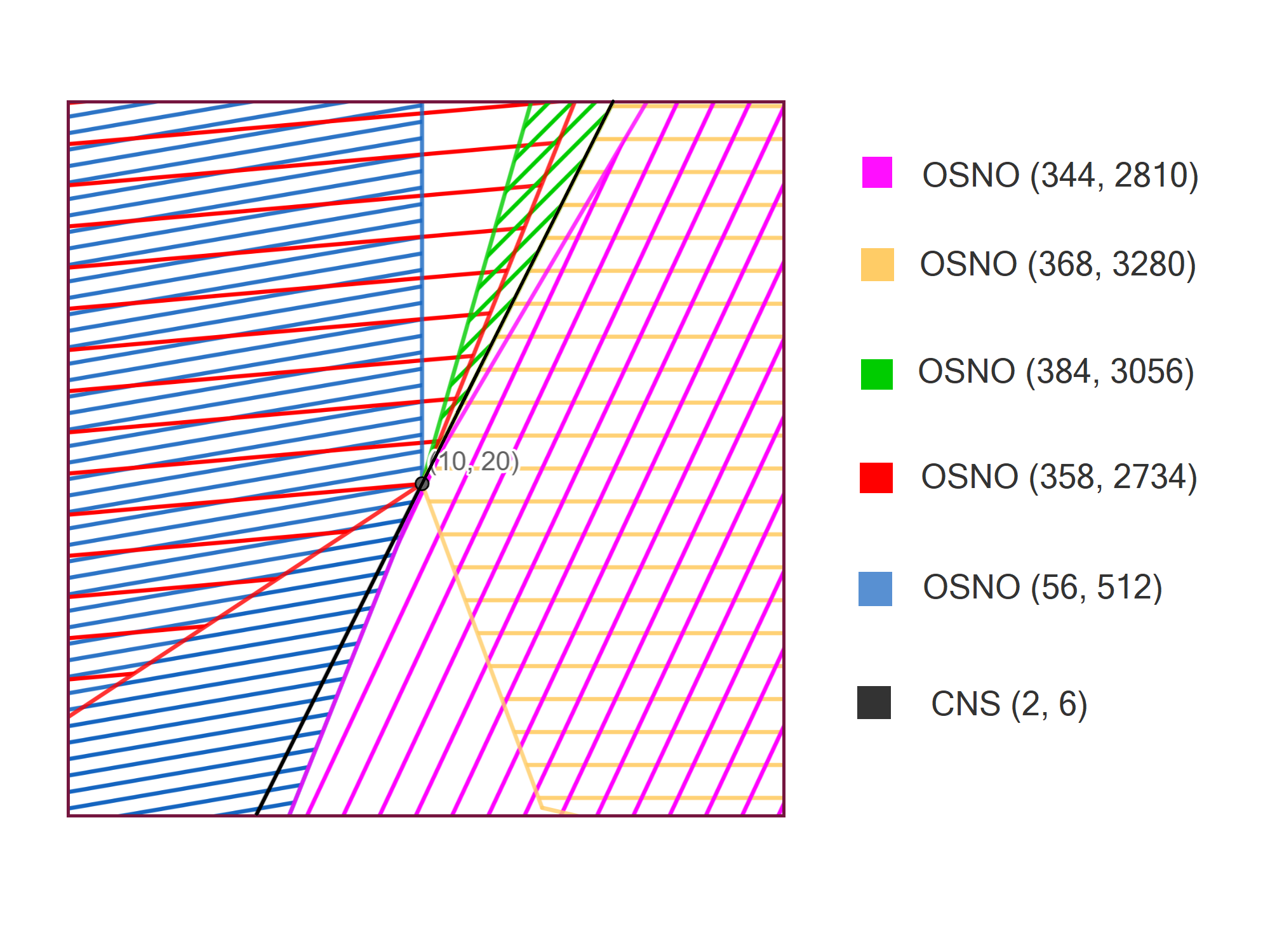
The hole at the interior point x=10, y=20 has now been covered. This point is the only known finite cover which is not on the boundary of the obtuse triangles and has no known stable point. This cover has five stables and one unstable to surround this point and uses the star rule algorithm and the golden square. All the obtuse triangles with any angle on the purple strip between 10 and 11 degrees are now all completely covered with periodic paths.

The Great Periodic Path Hunt

Find periodic paths in triangles and join the team. Can you find a periodic path of a billiard ball on an arbitrary triangular table given an arbitrary starting point and an arbitrary starting direction. Of particular interest are paths that hit sides perpendicularly. Does every obtuse triangle admit a periodic trajectory? and how can they be classified?

If you want to be a hunter, you need to download Billiards Everything.

History

The first examples of periodic orbits were discovered by Fagnano in 1745, who showed that all acute triangles have periodic orbits. Holt in 1993 did the same thing in all right-angled triangles. Masur in 1986 also did it for all rational triangles. Hooper and Schwartz in 2004 showed that all triangles with obtuse angle less than 100 degrees has a periodic path. Tokarsky and Marinov between 2005 and 2021 showed that any triangle with obtuse angle less than 112.4 degrees has a periodic path and also showed that any triangle with all angles greater than 11 degrees have a periodic path with the exception of one tiny flare around (15,30). We can now change the 11 degrees down to 10 degrees.

Special coverings

Special star square covered using star algorithm. Slide to see the OSNO 344 and OSNO 56 overlap.

OSNO 56 - 344 overlap.

Most current periodic paths coverings

August 27,2024 George Tokarsky, Letian Huang, Rui Huang, Austin Lu, Marco Mai and Kaiden Mastel covered the region with vertices (6,29), (10,25), (10,35), (6,39)

August 25,2023 George Tokarsky, Preet Gami, Max Godfrey, Kaixuan Hu, Letian Huang, Rui Huang, Rahul Korde, Boshen Lin, Kaiden Mastel, Khac Nguyen and Jaime Burgos Oteo covered the region with vertices (6,39), (10,35), (10,57.6), (6,61.6)

May 20,2022 Gurveer Singh Sohal covered the region with vertices (9,39),(10,38),(10,36.5),(9,37.5)

June 20,2021 Shehraj Singh covered the region with vertices (9,45),(10,44),(10,57.6),(9,58.6)

June 14,2021 Byron Tung covered the region with vertices (8,58),(9,57),(9,58.6),(8,59.6)

Tools

Billiards Everything is a computer program that finds periodic paths. It has both an experimental part and a proving part. The program started in 2005 by Tokarsky and Marinov and has been evolving ever since using laptops. We recommend that you download Billiards Everything and use the experimental part and send us the results and we will do the proving part on a supercomputer. Or if you just want to see the results and play around, you can download the two jars.

Downloads

You can download Billiards Everything and Billiards Covers from the SourceForge project page. The links are

Related theory

Lorenz Halbeisen and Norbert Hungerbuhler, "On Periodic Billiard Trajectories in Obtuse Triangles" SIAM Review 42, no. 4 (2000):657-670
Richard Evan Schwartz, "Obtuse Triangular Billiards II: One Hundred Degrees Worth of Periodic Trajectories", Experimental Mathematics 18, no. 2 (2009): 137-171.

Papers

George William Tokarsky and Boyan Marinov, "Obtuse Billiards" (pdf).

Documentation & Instructions

Here are the 2024 New instructions on finding and covering periodic paths (pdf). Here are the 2023 instructions on finding and covering periodic paths (pdf). Here are the old instructions on finding and covering periodic paths (pdf). Three videos follow.
A video showing the steps is at https://www.youtube.com/embed/kK12WIiIenA
An addendum video showing the AutoPolyVary is at https://www.youtube.com/embed/9xGWrUdvoHU
An addendum video showing the Triples and Factoring is at https://www.youtube.com/embed/ZB7Q2GoSCzk

Contributors

Summer 2024

Austin Lu
Bhavya Jain
Kaiden Mastel
Marco Mai

Summer 2023

Max Godfrey
Khac Nguyen
Jaime Burgos Oteo
Letian Huang
Rui Huang
Rahul Korde
Kaiden Mastel

Summer 2022

Marcus Gerrard
Shehraj Singh
Gurveer Singh Sohal
Xichen Pan

Summer 2021

Zijie Tan
Shiyu Xiu
Shehraj Singh
Byron Tung